Answer:
It takes 8.7 hours for there to be 3300 bacteria present.
Explanation:
Exponential equation for population growth:
The exponential equation for population growth is given by:
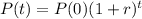
In which P(0) is the initial population and r is the growth rate.
2400 bacteria are placed in a petri dish.
This means that
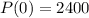
So
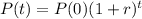
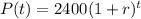
The conditions are such that the number of bacteria is able to double every 19 hours.
This means that
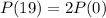 . We use this to find 1 + r.
. We use this to find 1 + r.
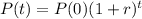
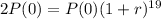

![\sqrt[19]{(1+r)^(19)} = \sqrt[19]{2}](https://img.qammunity.org/2022/formulas/mathematics/college/lgsgkdtzaskaoldf8llbyf9qbta21mm66r.png)
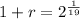
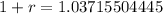
So
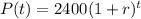
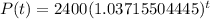
How long would it be, to the nearest tenth of an hour, until there are 3300 bacteria present?
This is t for which
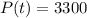 . So
. So
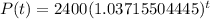

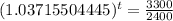
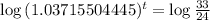
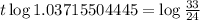
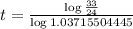
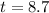
It takes 8.7 hours for there to be 3300 bacteria present.