Question

Robert must read a few books from his home library. He read any 4 out of 6 books from the top shelf, and then any 2 out of 3 books from the middle shelf and then any 3 out of 6 books from the bottom shelf. In how many ways can Robert read the books, if different orders in which the books will be read count as different ways

Answer 1

Robert can read the books in 129,600 different ways.

Explanation:

The order in which the book are read is important, which means that the permutations formula is used to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

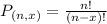
Top shelf:

4 books from a set of 6. So

`P_((6,4)) = (6!)/(2!) = 360`

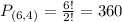
Middle shelf:

2 books from a set of 3. So

`P_((3,2)) = (3!)/(2!) = 3`

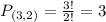
Bottom shelf:

3 books from a set of 6. So

`P_((6,3)) = (6!)/(3!) = 120`

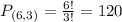
Total:

360*3*120 = 129,600

Robert can read the books in 129,600 different ways.