Question

a student standing in an elevator at rest notices that her pendulum has a frequency of oscillation of 0.5 Hz. a. what is the length of the pendulum's string? b. the elevator starts to accelerate upwards. what effect will this have on the oscillation? explain. ​

Answer 1

A) L = 0.496 m, B) the movement of the elevator upwards decreases the angular velocity of the pendulum

Step-by-step explanation:

A) The motion of a simple pendulum is a harmonic motion with angular velocity

w² = g /L

angular velocity and frequency are related

w = 2π f

we substitute

4π² f² = g /L

L =
`(g)/(4\pi ^2 f)`

let's calculate

L = 9.8 / 4 pi² 0.5

L = 0.496 m

B) To see the effect of the elevator acceleration (aₐ), let's use Newton's second law.

At the acceleration from the vertical direction upwards, let's decompose it is a component parallel to the movement and another perpendicular

sin θ = a_parallel / aₐ

a_parallel = aₐ sin θ

this component of the acceleration is in the opposite direction to the movement of the system, so it must be negative

- W sin θ = m (a - a_parallel)

- mg sin θ = m (
`(d^2 s)/(dt^2) - a_a sin \theta`)

all angles are measured in radians, therefore the angular displacement is

s = L θ

We solve the system for small angles

sin θ = θ

we substitute

- mg θ + m aₐ θ = m L
`(d^2 \theta)/(dt^2 )`

`- ( (g- a_a)/(L) ) \ \theta = (d^2 \theta)/(dT^2 )`

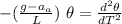
this is the same equation of the simple pendulum therefore the angular velocity is

w² =
`(g-a_a)/(L)`

When analyzing this expression, we see that the movement of the elevator upwards decreases the angular velocity of the pendulum