This question is incomplete, the complete question is;
For a steel alloy it has been determined that a carburizing heat treatment of 11.3 h duration at Temperature T1 will raise the carbon concentration to 0.44 wt% at a point 1.8 mm from the surface. A separate experiment is performed at T2 that doubles the diffusion coefficient for carbon in steel.
Estimate the time necessary to achieve the same concentration at a 4.9 mm position for an identical steel and at the same carburizing temperature T2.
Answer:
the required time to achieve the same concentration at a 4.9 is 83.733 hrs
Step-by-step explanation:
Given the data in the question;
treatment time t₁ = 11.3 hours
Carbon concentration = 0.444 wt%
thickness at surface x₁ = 1.8 mm = 0.0018 m
thickness at identical steel x₂ = 4.9 mm = 0.0049 m
Now, Using Fick's second law inform of diffusion
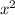 / Dt = constant
/ Dt = constant
where D is constant
then
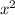 / t = constant
/ t = constant
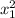 / t₁ =
/ t₁ =
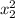 / t₂
/ t₂
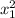 t₂ = t₁
t₂ = t₁
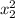
t₂ = t₁
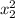 /
/
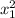
t₂ = (
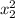 /
/
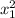 )t₁
)t₁
t₂ =

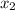 /
/

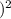 × t₁
× t₁
so we substitute
t₂ =
 0.0049 / 0.0018
0.0049 / 0.0018
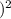 × 11.3 hrs
× 11.3 hrs
t₂ = 7.41 × 11.3 hrs
t₂ = 83.733 hrs
Therefore, the required time to achieve the same concentration at a 4.9 is 83.733 hrs