Question

Our environment is very sensitive to the amount of ozone in the upper atmosphere. The level of ozone normally found is 4.4 parts/million (ppm). A researcher believes that the current ozone level is at an insufficient level. The mean of 23 samples is 4.2 ppm with a standard deviation of 0.7. Does the data support the claim at the 0.01 level? Assume the population distribution is approximately normal. Step 1 of 5: State the null and alternative hypotheses.

Answer 1

To test the hypothesis is that the mean ozone level is different from 4.40 parts per million at 1% of significance level.

The null hypothesis and the alternative hypothesis is :

`$H_0: \mu = 4.40$`

`$H_a: \mu \\eq 4.40$`

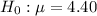
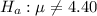
The z-test statistics is :

`$z=(\overline x - \mu)/(\left( \sigma / \sqrt n \right)) $`

`$z=(4.2 - 4.4)/(\left(0.7 / √(23) \right)) $`

`$z =(-0.2)/(0.145)$`

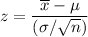
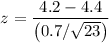
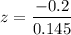
z = -1.37

The z critical value for the two tailed test at 99% confidence level is from the standard normal table, he z critical value for a two tailed at 99% confidence is 2.57

So the z critical value for a two tailed test at 99% confidence is ± 2.57

Conclusion :

The z values corresponding to the sample statistics falls in the critical region, so the null hypothesis is to be rejected at 1% level of significance. There is a sufficient evidence to indicate that the mean ozone level is different from 4.4 parts per million. The result is statistically significant.