Answer:
Slant height = 20 inches
Explanation:
To find the slant height of a triangular pyramid, we need to use the formula for the surface area of a triangular pyramid and then solve for the slant height.
The surface area (SA) of a triangular pyramid is given by:

In this case:
- S.A. = 305 in²
- Area of the base = 35 in²
- Perimeter of the base = 9 in + 9 in + 9 in = 27 in
Now, substitute these values into the surface area formula:

Now, solve for the slant height:
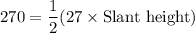
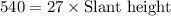
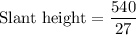
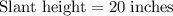
Therefore, the slant height of the triangular pyramid is 20 inches.