Question

During a testing process, a worker in a factory mounts a bicycle wheel on a stationary stand and applies a tangential resistive force of 130 N to the tire's rim. The mass of the wheel is 1.70 kg and, for the purpose of this problem, assume that all of this mass is concentrated on the outside radius of the wheel. The diameter of the wheel is 50.0 cm. A chain passes over a sprocket that has a diameter of 8.75 cm. In order for the wheel to have an angular acceleration of 3.50 rad/s2, what force, in Newtons, must be applied to the chain

Answer 1

The force that must be applied to the chain in order for the chain to have the given acceleration is approximately 694.2 N

Step-by-step explanation:

The given restive force,
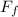`F_f` = 130 N

The mass of the wheel, m = 1.70 kg

The diameter of the wheel, D = 50.0 cm

∴ The radius of the wheel, R = 50.0 cm/2 = 25.0 cm = 0.25 m

The diameter of the sprocket over which the chain passes, d = 8.75 cm

The radius of the sprocket over which the chain passes, r = 8.75 cm/2 = 4.375 cm = 0.04375 m

The angular acceleration, α = 3.50 rad/s²

Torque, τ = I·α

Where;

I = The moment of inertia = m·R²·α

The net torque = The applied torque - The friction torque

Therefore, we get;

I × α = m × R² × α = F × r -
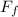`F_f` × R

1.70 kg × (0.25 m)² × 3.50 rad/s² = F × 0.04375 m - 120 N × 0.25 m

F = (1.70 kg × (0.25 m)² × 3.50 rad/s² + 120 N × 0.25 m)/(0.04375 m) = 694.214286 N

The force that must be applied to the chain in order for the chain to have the given acceleration, F ≈ 694.2 N