Question

Air initially at 120 psia and 500o F is expanded by an adiabatic turbine to 15 psia and 200o F. Assuming air can be treated as an ideal gas and has variable specific heat. a) Determine the specific work output of the actual turbine (Btu/lbm). b) Determine the amount of specific entropy generation during the irreversible process (Btu/lbm R). c) Determine the isentropic efficiency of this turbine (%).

Answer 1

a) specific work output of the actual turbine is 73.14 Btu/lbm

b) the amount of specific entropy generation during the irreversible process is 0.050416 Btu/lbm°R

c) Isentropic efficiency of the turbine is 70.76%

Step-by-step explanation:

Given the data in the question;

For an adiabatic turbine; heat loss Q = 0

For Initial State;

p₁ = 120 psia

T₁ = 500°F = 959.67°R

from table; { Gas Properties of Air }

At T₁ = 959.67°R

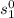`s_1^0` = 0.74102 Btu/lbm°R

`h_1` = 230.98 Btu/lbm

For Finial state;

p₂ = 15 psia

T₂ = 200°F = 659.67°R

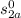`s^0_{2a` = 0.64889 Btu/lbm°R

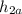`h_{2a` = 157.84 Btu/lbm

we know that R for air is 0.06855 Btu/lbm.R

a)

The specific work output of the actual turbine Wₐ is;

W
`_a` =
`h_1` -
`h_{2a`

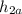
we substitute

W
`_a` = 230.98 - 157.84

W
`_a` = 73.14 Btu/lbm

Therefore, specific work output of the actual turbine is 73.14 Btu/lbm

b)

amount of specific entropy generation during the irreversible process.

To determine the entropy generation
`S_{gen`;

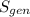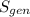`S_{gen` = ΔS =
`s_{2a` -
`s_1` =
`s^0_{2a` -
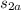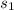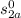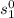`s_1^0` - R ln(
`(p_2)/(p_1)`)

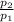we substitute in our values

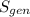`S_{gen` = 0.64889 - 0.74102 - 0.06855 ln(
`(15)/(120)`)

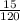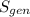`S_{gen` = 0.64889 - 0.74102 + 0.1425457

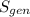`S_{gen` = 0.050416 Btu/lbm°R

Therefore, the amount of specific entropy generation during the irreversible process is 0.050416 Btu/lbm°R

c)

Isentropic efficiency of turbine η
`_{is`

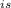
η
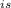`_{is` = {actual work output] / [ ideal work output ] = (
`h_1` -
`h_{2a` ) / (
`h_1` -
`h_{2s` )

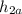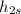Now, for an ideal turbine;

ΔS = 0 =
`s_{2s` -
`s_1`

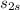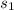
so,
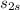`s_{2s` - s₁ =
`s^0_{2s` -
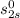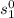`s_1^0` - R ln(
`(p_2)/(p_1)`)

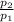0 =
`s^0_{2s` -
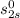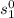`s_1^0` - R ln(
`(p_2)/(p_1)`)

`s^0_{2s` =
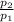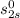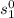`s_1^0` + R ln(
`(p_2)/(p_1)`)

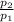we substitute

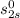`s^0_{2s` = 0.74102 + 0.06855 ln(
`(15)/(120)`)

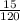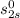`s^0_{2s` = 0.74102 - 0.1425457

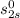`s^0_{2s` = 0.59847 Btu/lbm°R

Now, from table; { Gas Properties of Air }

At
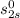`s^0_{2s` = 0.59847 Btu/lbm°R;
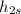`h_{2s` = 127.614 Btu/lbm

η
`_{is` = [(
`h_1` -
`h_{2a` ) / (
`h_1` -
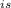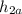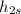`h_{2s` )] × 100%

we substitute

η
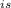`_{is` = [( 230.98 - 157.84 ) / ( 230.98 - 127.614 )] × 100%

η
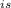`_{is` = [ 73.14 / 103.366] × 100%

η
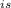`_{is` = 0.70758 × 100%

η
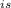`_{is` = 70.76%

Therefore, Isentropic efficiency of the turbine is 70.76%