Question

As you know a cube with each side 4 m in length has a volume of 64m3. Each side of the cube is now doubled in length. What is the ration if the new volume to the old volume

Answer 1

The ratio of the new volume to the old volume is 8 to 1.

Step-by-step explanation:

Let's first list what we know:

• A cube has sides with lengths of 4 m
• The volume of the cube is 64
  `m^3`
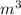
• The new cube has sides double the length of the old cube

Since the new cube has sides double the length of the sides of the old cube, and 4 doubled is 8, the length of the sides of the new cube is 8.

The equation for the volume of a cube is
`V = s^3`, where "V" is the volume and "s" is the lengths of the sides.

Now, let's solve for the volume of the new cube:

`V = s^3`

`V = 8^3`

`V = 512`

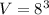
The volume of the new cube is 512
`m^3`.

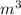The ratio of the new volume to the old volume is 512 : 64.

Let's simplify the ratio:

512 : 64

8 : 1

The ratio of the new volume to the old volume is 8 to 1.

P.S. This question should be in the mathematics subject, not the physics subject. (I pretty much only do math problems, so yes, it does matter. I don't know about the others though.)