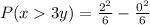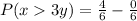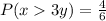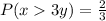Answer:
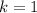
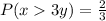
Explanation:
Given

Solving (a):
Find k
To solve for k, we use the definition of joint probability function:
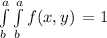
Where
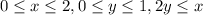
Substitute values for the interval of x and y respectively
So, we have:
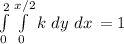
Isolate k

Integrate y, leave x:
![k \int\limits^2_(0) y {dx} \, [0,x/2]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/1sszuctxlzzd2zxuhcq87awoif6143eeq3.png)
Substitute 0 and x/2 for y
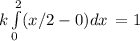

Integrate x
![k * (x^2)/(2*2) [0,2]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/ruhpack873dnsxek3xifr0gqa5msl84s9f.png)
![k * (x^2)/(4) [0,2]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/ur3ao9hba0nwgz26kz75frafkqfo0ran21.png)
Substitute 0 and 2 for x
![k *[ (2^2)/(4) - (0^2)/(4) ]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/qfbnp2hvsuovd0x8f9c0enu5dnbwqf5zey.png)
![k *[ (4)/(4) - (0)/(4) ]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/vidu5dzczu8tpmrrjo9ngm5etxjhttyk45.png)
![k *[ 1-0 ]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/oihocs49s4mfbdkt1ldxr36er507adx8fy.png)
![k *[ 1]= 1](https://img.qammunity.org/2022/formulas/mathematics/college/pudmf0j1sb56armrkvpucope4c6wlr4e6z.png)
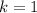
Solving (b):
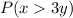
We have:
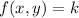
Where
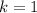
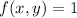
To find
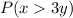 , we use:
, we use:
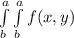
So, we have:

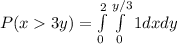
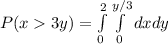
Integrate x leave y
![P(x > 3y) = \int\limits^2_0 x [0,y/3]dy](https://img.qammunity.org/2022/formulas/mathematics/college/s93owje02j9m6tz6vw9ifx3kh3560gzxn5.png)
Substitute 0 and y/3 for x
![P(x > 3y) = \int\limits^2_0 [y/3 - 0]dy](https://img.qammunity.org/2022/formulas/mathematics/college/pbomlenbgtvjeato7l4jkpk020e70e3fjx.png)
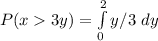
Integrate
![P(x > 3y) = (y^2)/(2*3) [0,2]](https://img.qammunity.org/2022/formulas/mathematics/college/wzu6nq5opskide3vm4xae01oe3knu5rd7y.png)
![P(x > 3y) = (y^2)/(6) [0,2]\\](https://img.qammunity.org/2022/formulas/mathematics/college/wemwrg08jazi2t5qt3a8ja9ogho71c2be3.png)
Substitute 0 and 2 for y