Question

Prove that 5root7 is i
rrational
​

Answer 1

See Explanation

Explanation:

Let us assume that
`5\sqrt 7` is a rational.

Therefore, it can be expressed in the form of
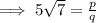
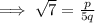
`(p)/(q)`, where p and q are integers.

`\implies 5\sqrt 7=(p)/(q)`

`\implies \sqrt 7=(p)/(5q)`

`\because` p and q are integers.

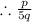`\therefore (p)/(5q)` is a rational number.

`\implies \sqrt 7` is rational (
`\because` quotient of a rational number is rational)

But, it contradicts the fact that
`\sqrt 7`is irrational.

So,
`5\sqrt 7` is also irrational, because the product of rational and irrational is irrational.

This contradiction is arising out because of our wrong assumption that
`5\sqrt 7` is rational.

Hence,
`5\sqrt 7` is irrational.