Question

In a magnetic sector (single-focusing) mass spectrometer, it might be reasonable under some circumstances to monitor one m/z value, to then monitor a second m/z. and to repeat this pattern in a cyclic manner. Rapidly switching between two accelerating voltages while keeping all other conditions constant is called peak matching

(a) Derive a general expression that relates the ratio of the accelerating voltages to the ratio of the corresponding m/z values.
(b) Use this equation to calculate m/z of an unknown peak if m/z of the ion used as a standard, CF3+, is 69.00 and the ratio of V unknown /V standard is 0.965035.
(c) Based on your answer in part (b), and the assumption that the unknown is an organic compound that has a mass of 143, draw some conclusions about your answer in part (b), and about the compound.

Answer 1

A) (m/Z)s / ( m/Z)u = Vu / Vs

B) 71.5

C) the ratio of accelerating voltages decrease as the value of the unknown mass increases.

Step-by-step explanation:

A) To derive the expression we have to vary one of the three variables while keeping the other two variables constant

let the variables be denoted as ; ( B , V , r )

m/z = B^2r^2e / 2v

therefore the equations can be written as

`( (m)/(z) )_(s) = (k)/(v_(s) )` ,
`( (m)/(z) )_(u) = (k)/(v_(u) )`

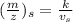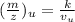
u = unknown value , s = standard value

∴ ratio of accelerating voltage to the ratio of corresponding m/Z values

= (m/Z)s / ( m/Z)u = Vu / Vs

B) find (m/Z) u

since : Vu / Vs = 0.965035

( m/Z) s = 69.00

Vu / vs = (m/Z)s / (m/Z)u -------- ( 1 )

∴ (m/Z)u = 69 / 0.965035 = 71.5

C) If the unknown mass ( m/z ) u = 143

the ratio of the voltages : Vu / vs = 69 / 143 = 0.4825

when compared to the answer gotten in b above it can be seen that the ratio of accelerating voltages decrease as the value of the unknown mass increases.