Question

A ball is thrown upward from a height of 15 feet with an initial velocity of 64 feet per second. Use indefinite integrals to write the position function of the ball at time t.

Answer 1

The equation of the position at time t will be:

`y(t)=-(1)/(2)9.81t^(2)+64t+15`

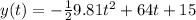
Explanation:

We can start by saying that the acceleration here is g = -9.81 m/s². The minus sign is because the gravity acceleration is a vector downward (negative value), and the ball is going upward (positive value).

And we know that acceleration can be written as a second derivative:

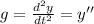`g=(d^(2)y)/(dt^(2))=y''` (1)

Now, we can take the integral in each side:

`\int gdt=\int y''dt`

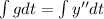
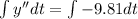`\int y''dt=\int -9.81dt` (2)

Solving the integral in each side we have:

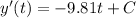`y'(t)=-9.81t+C` (3)

Where y'(t) is the velocity at t time (v = dy/dt = y' ) and c is a constant value.

Now, the initial conditions are:

initial height y(0) = 15 feet

initial velocity y'(0) = v(0) = 64 feet/s

Using this condition we can find C. Let's evaluate equation (3) at t = 0.

`y'(0)=-9.81(0)+C`

`C=64\: feet/s`

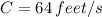
So we have:

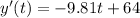`y'(t)=-9.81t+64` (4)

Now, we need to take the integral of equation (4) to get the position function:

`\int y'(t)dt=\int (-9.81t+64)dt`

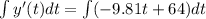
Solving this new integral we have:

`y(t)=-(1)/(2)9.81t^(2)+64t+D` (5)

Using the same method above, we can find D evaluating (5) at t = 0, we have:

`y(0)=-(1)/(2)9.81(0)^(2)+64(0)+D`

`D=y(0)`

`D=15\: feet`

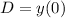
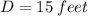
Finally, the equation of the position at time t will be:

`y(t)=-(1)/(2)9.81t^(2)+64t+15`

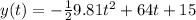
I hope it helps you!