Question

Consider the system of differential equations

dx/dt= x+ y=1
dy/dt =1- x^2 +y^2

Required:
Sketch the x-nullcline, where solutions must travel vertically. Identify the regions in the plane where solutions will move toward the right, and where solutions move toward the right.

Answer 1

Explanation:

Given that:

the differential equations:

`(dx)/(dt)= x+y = 1 \\ \\ (dy)/(dt)= 1-x^2+y^2`

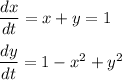
For x-nullcline;

`\implies (dx)/(dt) =0 \\ \\ \implies x+y-1`

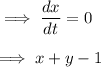
From the image attached below, the sketch of the x-nullcline was carefully drawn and the regions were identified.

So, x-increases at the time when
`(dx)/(dt)>0`

`\implies x+y -1 >0`

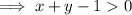
Thus, the solution move towards the right for x+y>1