Given:
The area of a rectangle =

Length of the rectangle =
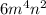
To find:
The width of the rectangle.
Solution:
Area of a rectangle is:
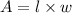
Where, l is the length and w is the width of the rectangle.
Divide both sides by l.
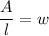
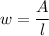
On substituting the given values, we get
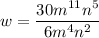

![[\because (a^m)/(a^n)=a^(m-n)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/is1hcfseg2iaix2ipewb8swtqj4tc0l7qq.png)
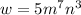
Therefore, the correct option is A.