Answer:
Probability that at least 490 do not result in birth defects = 0.1076
Explanation:
Given - The proportion of U.S. births that result in a birth defect is approximately 1/33 according to the Centers for Disease Control and Prevention (CDC). A local hospital randomly selects five births and lets the random variable X count the number not resulting in a defect. Assume the births are independent.
To find - If 500 births were observed rather than only 5, what is the approximate probability that at least 490 do not result in birth defects
Proof -
Given that,
P(birth that result in a birth defect) = 1/33
P(birth that not result in a birth defect) = 1 - 1/33 = 32/33
Now,
Given that, n = 500
X = Number of birth that does not result in birth defects
Now,
P(X ≥ 490) =
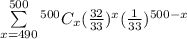
=
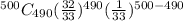 + .......+
+ .......+
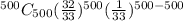
= 0.04541 + ......+0.0000002079
= 0.1076
⇒Probability that at least 490 do not result in birth defects = 0.1076