Question

What can you say about the end behavior of the function f(x) = -4x6+6x2 -52 ?

A. F(x)is an even function so both ends of the graph go in the same
direction.
B. f(x) is an even function so both ends of the graph go in opposite
directions
O C. The leading coefficient is negative so the left end of the graph
goes up.
D. The leading coefficient is negative so the left end of the graph
goes down

Answer 1

A. F(x)is an even function so both ends of the graph go in the same direction.

D. The leading coefficient is negative so the left end of the graph goes down.

Explanation:

Even function:

For every value of x, f(x) = f(-x)

In this question:

We are given the following function:

`f(x) = -4x^6 + 6x^2 - 52`

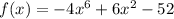
Testing if it is even:

`f(1) = -4(1)^6 + 6(1)^2 - 52 = -4 + 6 - 52 = -50`

`f(-1) = -4(-1)^6 + 6(-1)^2 - 52 = -4 + 6 - 52 = -50`

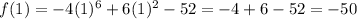
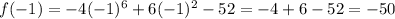
Since f(1) = f(-1), it is even.

Since it is even, both ends of the graph go in the same direction, so option A is correct, while option B is wrong.

Options C and D:

The leading coefficient, is -4(which multiplies x with the highest exponent). Since it is negative, it goes to negative infinity as x increases, that is, the left end goes down, and option D is correct while C is not.