Question

The straight line PQ with P(1,6) and Q(-6, 1). PQ is mapped onto P'Q' by a reflection in the line = 2. What are the coordinates of P

Answer 1

`P' = (1,-2)`

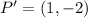
Explanation:

Given

`P = (1.6)`

`Q = (-6,1)`

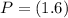
Reflection over:
`y = 2`

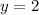
Required

Determine the coordinates of P'

From the given coordinates, the y coordinates of P is 6 and the line of reflection is at y = 2

Since we are to reflect over y = 2, only the y coordinate of P will be affected.

The idea behind reflecting a point over a line is to have an equal distance between [the original point & the line of reflection] and [the new point & the line of reflection]

So, what to do is:

First, calculate the difference between the y coordinates of P and the line of reflection.

The y coordinate of P is 6 and the line of reflection is at y = 2.

So, the difference is: 6 -2 = 4

Next, subtract the calculated difference from the line of reflection to get the y coordinate of P'

y coordinate of P' = 2 - 4 = -2

Hence, the coordinate of P' is: (1,-2)