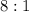Answer:
Lateral areas have ratio of 4:1
Volumes have ratio of 8:1
Explanation:
There is a rule in 3D geometry that when two solids are similar, and their edges are in the ratio of
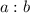 , the ratio of any surface area type measure is always
, the ratio of any surface area type measure is always
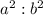 this includes the lateral area, which is just a surface area minus the base, which is not important for this problem. The ratio of volumes of those similar solids is in the ratio of
this includes the lateral area, which is just a surface area minus the base, which is not important for this problem. The ratio of volumes of those similar solids is in the ratio of
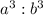 .
.
Now, to solve this, we need to find the ratio of any corresponding length of these similar pyramids. We have both the heights, so if we form a ratio of
 which if you simplify it, it is
which if you simplify it, it is
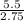 , which is
, which is
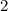 . The ratio of the heights are
. The ratio of the heights are
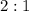 .
.
Now we can apply those rules to this ratio, the ratio of lateral areas would then be
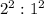 , which is
, which is
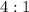 . the ratio of volumes would be
. the ratio of volumes would be
 , which is
, which is