Question

A copper wire loop has a circular shape, with a radius a (see below). The loop is put perpendicularly to the uniform magnetic field, which changes with time according to the next function (α and β are both constant and positive): B = α + βt. Is there an electromotive force induced in the loop? If yes, calculate its value and find its direction. If not, explain why there is no electromotive force induced in the loop.

Answer 1

fem = -A β

Step-by-step explanation:

Faraday's law gives the induced electromotive source (emf)

fem =
`- \ (d \phi_B )/(dt)`

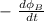
the magnetic flux is

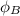`\phi_B` = B. A = B A cos θ

the bold are vectros. In this case the normal to the ring is parallel to the magnetic field so the angle is zero cos 0 = 1, also the area of the ring is constant

fem = -A
`(dB)/(dt)`

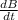
we carry out the derivative of the function B = α + β t

fem = -A β

so we see that there is an electromotive force in the ring.