Answer:
The original point is
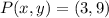 .
.
The distance between the points is 18 units.
Explanation:
The reflection of a point with respect to the x-axis is defined by the following operation:
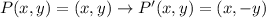 (1)
(1)
Where:
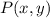 - Original point.
- Original point.
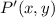 - Resulting point.
- Resulting point.
If we know that
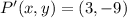 , then the original point is
, then the original point is
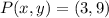 .
.
The original point is
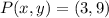 .
.
The distance between the points (
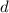 ), in units, is determined vectorially by the following expression, which is equivalent to the Pythagorean Theorem:
), in units, is determined vectorially by the following expression, which is equivalent to the Pythagorean Theorem:
![d = √([P'(x,y) -P(x,y)]\,\bullet\,[P'(x,y) -P(x,y)])](https://img.qammunity.org/2022/formulas/mathematics/high-school/pzfq91t43gwl2128i84yvghsl5ty98uj6h.png)
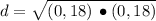
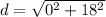
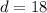
The distance between the points is 18 units.