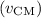Question

A group of particles of total mass 36 kg has a total kinetic energy of 398 J. The kinetic energy relative to the center of mass is 80 J. What is the speed of the center of mass

Answer 1

4.203 m/s

Step-by-step explanation:

First, we solve for the translational kinetic energy (
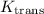`K_{\text {trans }}` ) in the definition of the total kinetic energy
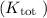`\left(K_{\text {tot }}\right)`. We also have an equation for the definition of
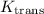`K_{\text {trans }}` (third line). From these two equations we can solve for the speed of the center of mass
`\left(v_{\mathrm{CM}}\right)`

`\begin{aligned} </p><p>K_{\text {tot }} &=K_{\text {trans }}+K_{\text {rot }} \\ </p><p>\Longrightarrow K_{\text {trans }} &=K_{\text {tot }}-K_{\text {rot }} \\ </p><p>K_{\text {trans }} &=(1)/(2) m_{\text {tot }} v_{\mathrm{CM}}^(2) \\ </p><p>\Rightarrow (1)/(2) m_{\text {tot }} v_{\mathrm{CM}}^(2) &=K_{\text {tot }}-K_{\text {rot }} \\ </p><p>\Rightarrow v_{\mathrm{CM}} &=\sqrt{\frac{2\left(K_{\text {tot }}-K_{\text {rot }}\right)}{m_{\text {tot }}}} \\ </p><p>&=\sqrt{\frac{2(398 \mathrm{~J}-80 \mathrm{~J})}{36 \mathrm{~kg}}}=4.203 \frac{\mathrm{m}}{\mathrm{s}} </p><p>\end{aligned}`