Answer:
The first derivative of
 is
is
 .
.
Explanation:
Let
 . we can determine its first derivative by Rule for the Square Root Function, Rule for Power Function, Rule of Chain and Rule for the Addition of Functions, Rule for the Subtraction of Functions, Rule for the Division of Functions:
. we can determine its first derivative by Rule for the Square Root Function, Rule for Power Function, Rule of Chain and Rule for the Addition of Functions, Rule for the Subtraction of Functions, Rule for the Division of Functions:
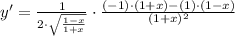
![y' = (1)/(2)\cdot \sqrt{(1+x)/(1-x) }\cdot \left[(-1-x-1+x)/((1+x)^(2)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2h6atwmug92i5f3pazg6p4rhg356n0vfpb.png)
![y' = (1)/(2)\cdot \sqrt{(1+x)/(1-x) } \cdot \left[-(2)/((1+x)^(2)) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/fqartsu8c3i93oiciq70kom504jbd0gyy9.png)

The first derivative of
 is
is
 .
.