Question

Triangle DEF has vertices D(0,0), E(7,0), and F(3,7).

The altitudes of triangle DEF intersect at point

Answer 1

(3, 1.7)

Explanation:

The point at which the vertices of a triangle meet is known as the orthocenter of the triangle. The orthocenter passes through the vertex of the triangle and is perpendicular to the opposite sides.

Two lines are perpendicular if the product of their slopes is -1.

The slope of the line joining D(0,0), F(3,7) is:

`m_1=(7-0)/(3-0)=(7)/(3)`

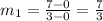
The slope of the line perpendicular to the line joining D and F is -3/7. The orthocenter is perpendicular to the line joining D and F and passes through vertex E(7, 0). The equation is hence:

`y-y_1=m(x-x_1)\\\\y-0=-(3)/(7) (x-7)\\\\y=-(3)/(7)x+3 \ .\ .\ .\ (1)`

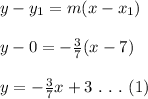
The slope of the line joining E(7,0), and F(3,7). is:

`m_1=(7-0)/(3-7)=-(7)/(4)`

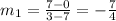
The slope of the line perpendicular to the line joining E and F is 4/7. The orthocenter is perpendicular to the line joining E and F and passes through vertex D(0, 0). The equation is hence:

`y-y_1=m(x-x_1)\\\\y-0=(4)/(7) (x-0)\\\\y=(4)/(7) x\ .\ .\ .\ (2)`

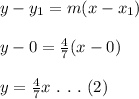
The point of intersection of equation 1 and equation 2 is the orthocenter. Solving equation 1 and 2 simultaneously gives:

x = 3, y = 1.7