Solve the Quadratic equation

Question

asked Jun 8, 2022 41.1k views

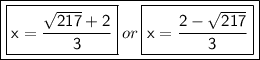
2 Answers

Bhaskar Vaddadi · Answer 1 · 2022-06-12T16:05:04+0000

Answer:

$\boxed{\boxed{\sf x=(√(217) +2)/(3) }\:or\: {\sf\boxed{\sf x=(2-√(217) )/(3) } }}$

Explanation:

$\boxed{\sf Quadratic \:equation}$

*All equations of the form ax^2+bx+c=0 can be solved using the Quadratic Formula. *

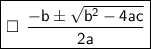
$\boxed{\sf \square \: \:(-b\pm √(b^2-4ac))/(2a)}$

The Quadratic Formula gives two solutions, one when ± is addition and one when its subtraction.

________________________________

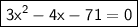
$\boxed{\sf 3x^2-4x-71=0}$

This equation here is in the standard form: ax^2+bx+c=0.

Substitute 3 → a, -4 → b, -71 → c.

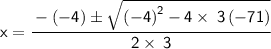
$\sf x=\cfrac{-\left(-4\right)\pm √(\left(-4\right)^2-4* \:3\left(-71\right))}{2* \:3}$

→ Square -4, and then multiply -4 × 3= :

$x=\cfrac{-(-4)\pm √(16+12(-71)) }{2* 3}$

Multiply -12 × -71 = 868, then Add 16+852= 868

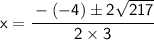
$\sf x=\cfrac{-(-4)\pm 2√(217) }{2* 3}$

Take the Square root of 868 2√(217).

* the opposite of -4 → 4.

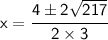
$\sf x=\cfrac{4\pm 2√(217) }{2* 3}$

Multiply 2 × 3 = 6

$\sf x=\cfrac{4\pm 2√(217) }{6}$

Now, we'll solve the equation when ± is plus.

→ Add 4+ 2√(217).

→ Divide 4+ 2√(217 ) by 6.

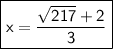
$\boxed{\sf x=(√(217) +2)/(3) }$

Now, we'll solve the equation when ± is minus.

→ Subtract 2√(217) from 4.

→ Divide 4 - 2√(217) by 6.

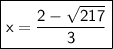
$\boxed{\sf x=(2-√(217) )/(3) }$

_________________________________________