Answer:
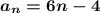
========================================================
Step-by-step explanation:
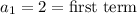
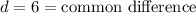
The common difference is 6 because we add 6 to each term to get the next term.
Or you can subtract adjacent terms to determine the common difference.
- d = term2-term1 = 8-2 = 6
- d = term3-term2 = 14-8 = 6
Be sure to keep the order of subtraction consistent. Always subtract off the previous term. Note that the sequence is increasing, so the value of d must be positive.
We'll use the values
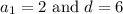 to determine the nth term formula of this arithmetic sequence.
to determine the nth term formula of this arithmetic sequence.
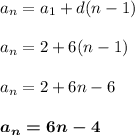
which is the final answer.
Then as partial verification, we can plug in positive integers for n to get corresponding terms.
For instance, plug in n = 3 to find that:
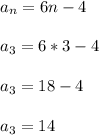
Telling us that the 3rd term is 14, which matches what the instructions mentioned. I'll let you confirm the other terms.