Question

Factor binomial
x²-36=​​

Answer 1

Answer: (x - 6)(x + 6)

Explanation:

To factor this, recall the difference of squares

`a^(2) - b^(2) = (a-b)(a+b)`

And because 36 is
`6^(2)`, that means

`x^(2) - 36 = x^(2) - 6^(2) = (x-6)(x+6)`

Answer 2

`\bold{(x-6)(x+6)}`

To simplify this equation, quadratic factoring patterns should be used. These patterns are the following:

`\bold{a^2-b^2=(a-b)(a+b)}`

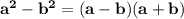
This pattern works because if one distributes the terms in the parentheses by multiplying each term in one of the parentheses by each term in the other, the result is the original equation:

`\bold{36=6^2}`

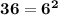
So it can be applied to the given equation:

`\bold{x^2-36}`

`\bold{ \bold{\boxed{(x-6)(x+6)}}}`

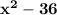
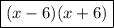
The factored form of the expression is
`\bold{(x-6)(x+6)}`