Question

Find the vertex:
x^2+x-6=0

Answer 1

`\left(-(1)/(2), -(25)/(4)\right)`

Explanation:

The vertex of a quadratic equation is the point at which the corresponding quadratic function reaches its maximum or minimum value, depending on the direction of the parabolic curve. It is the maximum point if the parabola opens downward, or the minimum point if the parabola opens upward.

`\boxed{\begin{array}{l}\underline{\sf Vertex\;form\;of\;a\;quadratic\; equation}\\\\y=a(x-h)^2+k\\\\\sf where:\\ \phantom{ww}\bullet\;(h,k)\;\sf is\;the\;vertex.\\\phantom{ww}\bullet\;a\;\sf is\;some\;constant.\\\end{array}}`

To find the vertex of the given quadratic equation x² + x - 6 = 0, first express it in the standard vertex form y = a(x - h)² + k and then identify the values of h and k.

Given equation:

`x^2 + x - 6 = 0`

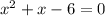
Complete the square to rewrite the equation in vertex form:

`\begin{aligned}x^2+x-6&=0\\\\x^2+x-6+6&=0+6\\\\x^2+x&=6\\\\x^2+x+\left((1)/(2)\right)^2&=6+\left((1)/(2)\right)^2\\\\x^2+x+(1)/(4)&=6+(1)/(4)\\\\x^2+x+(1)/(4)&=(25)/(4)\\\\\left(x+(1)/(2)\right)^2&=(25)/(4)\\\\\left(x+(1)/(2)\right)^2-(25)/(4)&=(25)/(4)-(25)/(4)\\\\\left(x+(1)/(2)\right)^2-(25)/(4)&=0\end{aligned}`

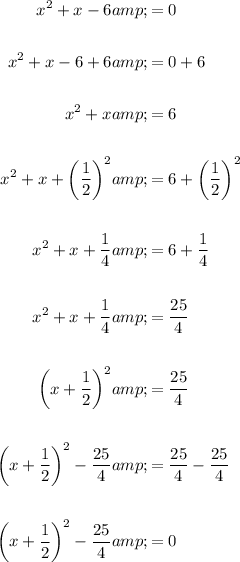
Now, the equation is in the form (x - h)² - k = 0, where:

`h = -(1)/(2)`

`k = -(25)/(4)`

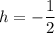
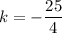
The vertex is (h, k).

Therefore, the vertex is:

`\left(-(1)/(2), -(25)/(4)\right)`