Question

If
f(x) = 2x² – 5
and
g(x) = 5x + 7
Find
g(f(x)) = 10x² + [? ]

Answer 1

The missing term in the output of the function
`g(f(x))` is -18.

`g(f(x))=10x^2-18`

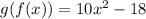
Explanation:

Function Composition

In mathematics, function composition is a term that encompasses a relationship between two functions wherein the output of one function is used as the input for another function. This relationship combines two functions to form a single function, known as a composite function. For future reference, function composition may also be denoted by a small circle, see below:

`(g\circ f)(x)=g(f(x))`

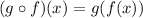
In the given problem, we must evaluate the composite function
`g(f(x))` /
`(g\circ f)(x)` to identify the unknown term.

With composite functions, we begin evaluating from the inside. To evaluate
`g(f(x))`, we must substitute the output of the function
`f(x)` (given as the expression
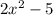`2x^2-5`) as the input (
`x`) for the function
`g(x)`:

`g(f(x))=g(2x^2-5)`

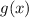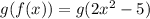
Now, using
`f(x)` as the input (
`x`) for the function
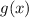`g(x)` (given as the expression
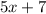`5x+7`), we can substitute
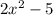`2x^2-5` into the output for the function
`g(x)`:

`g(f(x))= 5(2x^2-5)+7`

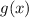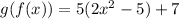
From here, we can go ahead and distribute the 5:

`g(f(x))=10x^2-25+7`

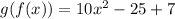
Combine like terms:

`g(f(x))=10x^2-18`

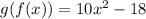
With the composite function evaluated, we can identify our missing term as
`-18`.