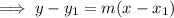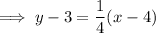Question

Write an equation of the line that passes through the given point and is (a) parallel and (b) perpendicular to the given line.

Answer 1

`\textsf{a)} \quad y=-4x+19`

`\textsf{b)} \quad y=(1)/(4)x+2`

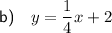
Explanation:

From inspection of the graph, two points on the line are:

• (1, 6)
• (2, 2)

Substitute these points in the slope formula to find the slope of the line:

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(2-6)/(2-1)=(-4)/(1)=-4`

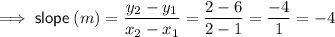
Part (a)

Lines that are parallel have the same slope.

Therefore, a line parallel to the given line has a slope of -4.

To write an equation of the parallel line, substitute the found slope and point (4, 3) into the point-slope formula and rearrange:

`\implies y-y_1=m(x-x_1)`

`\implies y-3=-4(x-4)`

`\implies y-3=-4x+16`

`\implies y=-4x+19`

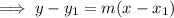
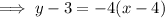
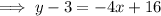
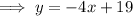
Part (b)

If two lines are perpendicular to each other, their slopes are negative reciprocals.

Therefore, a line perpendicular to the given line has a slope of ¹/₄.

To write an equation of the parallel line, substitute the found slope and point (4, 3) into the point-slope formula and rearrange:

`\implies y-y_1=m(x-x_1)`

`\implies y-3=(1)/(4)(x-4)`

`\implies y-3=(1)/(4)x-1`

`\implies y=(1)/(4)x+2`