Answer:
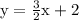
This is the same as writing y = (3/2)x + 2
=====================================================
Work Shown:
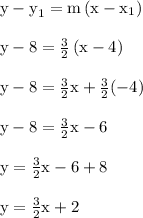
I used point-slope form as the first step. The 'm' is the slope, and
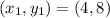 is the point on the line.
is the point on the line.
The final step shows us the line has a y intercept of b = 2, which is at the location (0,2).
To graph this, draw a straight line through (0,2) and (4,8)
--------------
Check:
Plug x = 4 into the equation we found. We should arrive at y = 8.
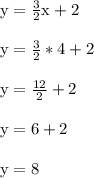
This confirms (4,8) is indeed on this line and confirms the answer is correct.
You can also use graphing tools like Desmos or GeoGebra to quickly and visually confirm the answer.