Question

Rewrite the expression with rational exponents as a radical expression by extending the properties of integer exponents:

three to the one third power all over three to the one sixth power
A. the square root of three to the one sixth power
B. the ninth root of three squared
C. the square root of three to the sixth power
D. the sixth root of three

Answer 1

D. The sixth root of three

Explanation:

Translate from words to math symbols:

three to the one third power all over three to the one sixth power

`\frac{3^{(1)/(3) } }{3^{(1)/(6) } } \\`

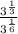
Rewrite the expression with rational exponents as a radical expression by extending the properties of integer exponents:

`\frac{\sqrt[3]{3} }{\sqrt[6]{3} }`

Simplify:

`\frac{\sqrt[3]{3} }{\sqrt[6]{3} } = \frac{\sqrt[3]{3} }{\sqrt[6]{3} } * \frac{\sqrt[6]{3^(5) } }{\sqrt[6]{3^(5) } } = \frac{\sqrt[3]{3} *\sqrt[6]{3^(5) } }{\sqrt[6]{3^(6) } } = \frac{3^{(1)/(3) }*3^{(5)/(6) } }{3^{(6)/(6) } } = \frac{3^{((1)/(3) +(5)/(6) )} }{3} = \frac{3^{((2)/(6) +(5)/(6) )} }{3} = \frac{3^{(7)/(6) } }{3} = \frac{3^{(1)/(6) } *3}{3} = \\\\3^{(1)/(6) } = \sqrt[6]{3}`

Answer:

`\sqrt[6]{3}`

D. the sixth root of three