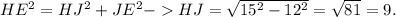Question

7. The perpendicular bisectors of
AEFG meet at point H. Find HJ.

Answer 1

The distance of the intersection of 3 perpendicular bisectors of a triangle to the 3 vertices are equal.

In other words, HF = HE = HG.

Therefore, we see that 3 isosceles triangles are identified : HFE, HFG, HGF.

We're given HF = 15, therefore HE = 15.

Since HJ is the perpendicular bisector of line EG, JE = JG.

Therefore, JE = 12.

Now, we use the Pythagorean theorem in the right triangle HJE :


`HE^(2) = HJ^(2) + JE^(2) - > HJ = \sqrt{15^(2) - 12^(2) } =√(81) = 9.`