Answer:
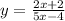
Explanation:
So we have the equation:

I'm assuming this is the result of finding an inverse function, and this may seem tricky at a glance, but generally whenever we have a function with two y's, we want to somehow factor out the y.
To achieve this, let's first remove the denominator by multiply both sides by (5y - 2)
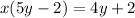
Now let's distribute the 5y - 2
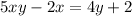
Remember, our goal is to factor out the y, so let's move all the terms with "y" on one side, and all the terms without "y" on the other side. So add 2x to both sides.
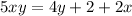
Now from here subtract 4y from both sides
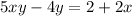
Now from here, we can finally factor out y on the left side
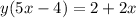
Notice, we now only have one y term, so from here it's easy to solve the equation! We simply divide both sides by (5x - 4) to isolate this y term
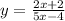
and now we get our final answer!