Question

Use the discriminant to describe the type and number of roots of 9x^(2) + 3x - 2 = 0

The quadratic equation has one imaginary and one real number root.
The quadratic equation has two distinct real number roots.
The quadratic equation has two complex number roots.
The quadratic equation has one real number root.

Answer 1

b) The quadratic equation has two distinct real number roots.

Explanation:

Rule: If the discriminant (
`b^2 - 4ac`) :

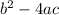is = 0, one root

is > 0, 2 real roots

is < 0, 0 real root, 2 complex roots.

-The reason is because complex numbers include imaginary numbers, which occur when you try to calculate the square root of a negative number.

Lets find the discriminant.

a: 9

b: 3

c: -2

Plug into the formula.

(3)^2 - 4(9)(-2)

Simplify.

9 + 72

81

Because the discriminant (81) is greater than 0, it has 2 real number roots.