Question

(a) Find the expectation E (X) of X.E(x) = 1(b) Find the variance Var(x) of x.Var(x) = 1

Answer 1

Part a.

The expected value is calculated by multiplying eacn of the possible outcomes by their respective probability and then summing all of those values. In our case, we have

`\begin{gathered} E(X)=\sum_^X_i* P(X_i) \\ \end{gathered}`

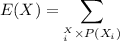
then

`E(X)=2*0.05+3*0.30+4*0.10+5*0.15+6*0.35+7*0.05`

which gives

`E(X)=4.6`

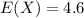
Part b

On the other hand, the sample variance is computed as

`Var(X)=\sum_{j\mathop{=}1}^n(x_i^2*P(X_i)^-\mu^2`

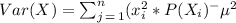
where μ is the mean value. Given by

`\mu=(2+3+4+5+6+7)/(6)=4.5`

So we get

`\begin{gathered} Var(X)=4*0.05+9*0.3+16*0.1+25*0.15+36*0.35+49*0.05-4.5^2 \\ Var(X)=23.3-20.25 \end{gathered}`

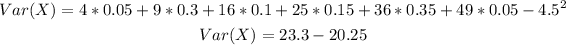
which gives

`Var(X)=3.05`

Therefore, the answers are:

a) E(X)= 4.6

b)

Var(X)=3.05