Question

Give the following equations determine if the lines are parallel perpendicular or neither

Answer 1

In order to determine whether the equations are parallel, perpendicular, or neither, let's simply each equation into a slope-intercept form or basically, solve for y.

Let's start with the first equation.

`(6x-5y)/(2)=x+1`

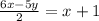
Cross multiply both sides of the equation.

`6x-5y=2(x+1)`
`6x-5y=2x+2`

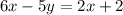
Subtract 6x on both sides of the equation.

`6x-5y-6x=2x+2-6x`
`-5y=-4x+2`

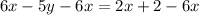
Divide both sides of the equation by -5.

`-(5y)/(-5)=(-4x)/(-5)+(2)/(-5)`
`y=(4)/(5)x-(2)/(5)`

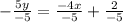
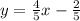
Therefore, the slope of the first equation is 4/5.

Let's now simplify the second equation.

`-4y-x=4x+5`

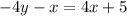
Add x on both sides of the equation.

`-4y-x+x=4x+5+x`
`-4y=5x+5`

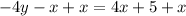
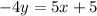
Divide both sides of the equation by -4.

`(-4y)/(-4)=(5x)/(-4)+(5)/(-4)`
`y=-(5)/(4)x-(5)/(4)`

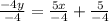
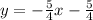
Therefore, the slope of the second equation is -5/4.

Since the slope of each equation is the negative reciprocal of each other, then the graph of the two equations is perpendicular to each other.