Question

Graphing QuadraticsQuestion 1 (2 points)(03.04)For the function f(x) = -2(x + 3)2 -1, identify the vertex, domain, and range. (2 points)аThe vertex is (3,-1), the domain is all real numbers, and the range is y> -1.The vertex is (3,-1), the domain is all real numbers, and the range is y < -1.оооThe vertex is (-3,-1), the domain is all real numbers, and the range is y < -1.aanThe vertex is (-3,-1), the domain is all real numbers, and the range is y 2-1.

Answer 1

The given function is:

`f(x)=-2(x+3)^2-1`

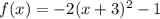
This is a quadratic function or parabola writen in "vertex form"

From the general structure of the vertex form we know that:

`f(x)=a(x-h)^2+k`

"h" is the x-coordinate of the vertex, in the formula it appears with the sign inverted, this means that if the value is positive, the coordinate will ve negative, or, if the value is negative, then the coordinate will be positive.

"k" is the y-coordinate of the vertex

The sign of "a" indicates if the parabola opens upwards or downwards.

If a is negative → the parabola opens downwards

If a is positive → the parabola opens upwards

So, for the given function:

From this we can determine that the vertex of the quadratic function is:

V(-3,-1)

And its range is

[-∞≤y≤-1] or y≤-1

The domain of these type of functions is all real numbers