Question

An iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylinderical part is 240 cm high and the conical part in 36 cm high. Find the weight of the pillar if one cu. cm of iron weighs 7.8 grams.

Answer 1

The iron pillar should look like this

The volume of the cylindrical part = πr²h

`V=\pi r^2h=(22)/(7)*8*240=(337920)/(7)\text{ cm}^3`

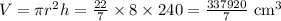
The volume of the conical part = 1/3 x base area x height

`V_(Cone)=(1)/(3)*(22)/(7)*8^2*36=(16896)/(7)\text{ cm}^2`

Therefore, Total volume

`TV=V+V_(Cone)=(337920)/(7)+(16896)/(7)=50688\text{ cm}^2`

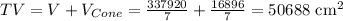
Mass = Density x Volume

= 7.8 x 50688

= 395366.4 g

= 395.3664 kg

Weight = 395.3664 x 10 = 3953.664 N