Question

1. A young tree is supported by two wires one on either side of the tree, that meet at the trees trunkand form a 80°angle. The longer wire connected to a stake on the right side of the tree and makesa 40° with the ground. If the stake holding the shorter wire is 12 feet away from the stake holdingthe longer wires in the ground, how long is each wire?

Answer 1

From the diagram provided in the question, we have the following triangle:

We have the following angle and side measures:

`\begin{gathered} z=80\degree \\ y=40\degree \\ G=12\text{ feet } \\ x=180-80-40=60\degree\text{ (Sum of angles in a triangle)} \end{gathered}`

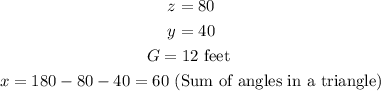
Recall the Sine Rule:

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

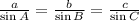
Comparing to our triangle, we have the sine rule applied as:

`(L)/(\sin x)=(G)/(\sin z)=(S)/(\sin y)`

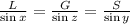
Length of Longer Wire (L):

`(L)/(\sin x)=(G)/(\sin z)`

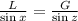
Substituting the given values, we have:

`\begin{gathered} (L)/(\sin60)=(12)/(\sin 80) \\ L=(12\sin 60)/(\sin 80) \\ L=10.55\text{ feet} \end{gathered}`

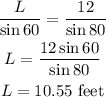
The length of the longer wire is approximately 10.6 feet.

Length of Shorter Wire (S):

`(G)/(\sin z)=(S)/(\sin y)`

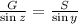
Substituting known values, we have:

`\begin{gathered} (12)/(\sin80)=(S)/(\sin 40) \\ S=(12\sin 40)/(\sin 80) \\ S=7.83\text{ feet} \end{gathered}`

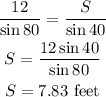
The length of the shorter wire is approximately 7.8 feet.