We know that the acceleration is defined as:
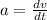
This means that if we know the acceleration we can find the velocity with the integral:
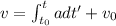
where t0 denotes some intial time and v0 the velocity at that time.
In this case we know that the acceleration is 4m/s^2 and that at time t=1 the velocity is 4 m/s, then we have:
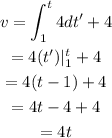
hence the velocity function for this motion is:
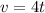
Now, we know that the velocity is defined by:
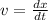
then the position can be obtained by:
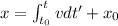
where t0 is some time and x0 is the position at that time; in this case we don't have an initial position for the particle then te position will be given by:
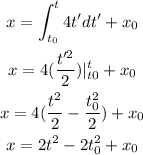
Hence the position at any given time is given by:
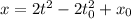
Once we know the position function we can calculate the area undert the position time graph in the interval given:
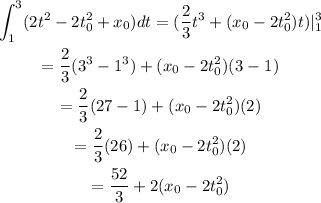
Therefore, in general, the area under the curve in the given interval is:
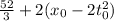
If we assume that the particle was at the origin at time t0=0 (this meas x0=0 as well), then the area under the position-time graph will be:
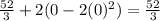
Note: No matter what the intial time and position is the expression we found will give us the correct answer.