Question

The spread of a highly contagious virus in a high school can be described by the logistic functiony=36001+899e−0.6xwhere x is the number of days after the virus is identified in the school and y is the total number of people who are infected by the virus.(a) Graph the function for 0≤x≤15.(b) How many students had the virus when it was first discovered?(c) What is the upper limit of the number infected by the virus during this period?

Answer 1

Given the function:

`y=(3600)/(1+899e^(-0.6x))`

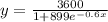
Let's solve for the following:

(a) Graph the function for 0≤x≤15.

This is an exponential function.

This graph will stop increasing at y = 3600

Thus, we have the graph below:

The graph that correctly represents this situation is graph C.

(b) How many students had the virus when it was first​ discovered?

Here, we are to find the y-intercept.

At the y-intercept, the value of x is zero.

Now, substitute 0 for x and solve for y:

`\begin{gathered} y=(3600)/(1+899e^(-0.6x)) \\ \\ y=(3600)/(1+899e^(-0.6(0))) \\ \\ y=(3600)/(1+899e^0) \\ \\ y=(3600)/(1+899) \\ \\ y=(3600)/(900) \\ \\ y=4 \end{gathered}`

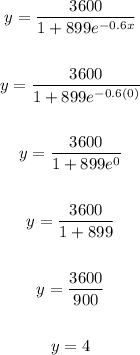
Therefore, the number of students that had the virus when it was first discovered is 4.

(c) What is the upper limit of the number infected by the virus during this​ period?

Here, we have the limit 0≤x≤15.

This means the upper limit infected during this period will be at x = 15 .

Substitute 15 for x and solve:

`\begin{gathered} y=(3600)/(1+899e^(-0.6(15))) \\ \\ y=\frac{3600^{}}{1+899(0.0001234)} \\ \\ y=3240.48 \end{gathered}`

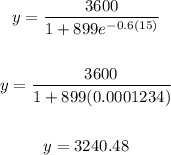
Therefore, the upper limit of the number infected by this virus in [0, 15] is 3240.48

ANSWER:

(b) 4 students

(c) 3240.48