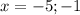Question

I need help with a graph problem please that I am stuck on.

Answer 1

First we have to derive the equation of the graph plot.

The general equation of an absolute value function is expressed as

`\begin{gathered} y=a|x-h|+k\text{ --- equation 1} \\ \text{where} \\ (h,k)\text{ is the coordinate of the vertex of the function } \end{gathered}`

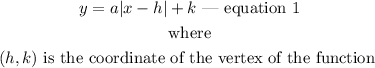
step 1: Determine the coordinates (h,k) of the vertex of the graph.

The vertex of the function is the point at which the graph changes direction.

In tha above plot, the vertex of the plot is (-3,4).

Thus,

`\begin{gathered} h=-3 \\ k=4 \end{gathered}`

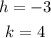
step 2: Substitute the respective values of -3 and 4 for h and k into equation 1.

Thus,

`\begin{gathered} y=a|x-h|+k \\ \Rightarrow y=a|x-(-3)|+4\text{ ---- equation 2} \\ \end{gathered}`

step 3: Select any point (x,y) on the graph plot, to evaluate a.

Thus, using the point (1,0), we have

`\begin{gathered} y=a|x+3|+4 \\ x=1,\text{ y=0} \\ \Rightarrow0=a|1+3|+4 \\ -4=|4|a \\ \Rightarrow a=-1 \end{gathered}`

step 4: Substitute the obatined value of a into equation 2.

Thus,

`y=-|x+3|+4\text{ ----- equation 3}`

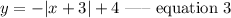
Thus, the equatioin of the graph is evaluated to be

`y=-|x+3|+4`

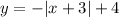
A) Evaluate f(4).

To evaluate f(4), substitute the value of 4 for x into the derived equation.

Thus,

`\begin{gathered} y=-|x+3|+4 \\ x=4 \\ \Rightarrow y=-|4+3|+4 \\ \therefore y=-3 \end{gathered}`
`f(4)=-3`

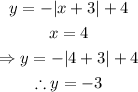
B) Solve for f(x)=2.

To solve, we have

`\begin{gathered} -|x+3|+4=2 \\ \text{subtract 4 from both sides of the equation} \\ -|x+3|+4-4=2-4 \\ -|x+3|=-2 \\ \text{divide both sides by -1} \\ (-|x+3|)/(-1)=-(2)/(-1) \\ \Rightarrow|x+3|=2 \\ \text{When }x+3=-2 \\ x=-2-3 \\ \Rightarrow x=-5 \\ \text{when }x+3=2 \\ x=2-3 \\ \Rightarrow x=-1 \end{gathered}`

Thus, we have

`x=-5;-1`