Question

Special right triangle find the value of the variables answer must be in simplest radical form

Answer 1

Here, we have a special right triangle.

Let's solve for the variables, x and y.

Given:

common side = x

Hypotenuse of the larger triangle = 8

Let's find x using trigonometric ratio.

We have:

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \\ \sin 30=(x)/(8) \\ \\ x=8\sin 30 \\ \\ x=8(0.5) \\ \\ x=4 \end{gathered}`

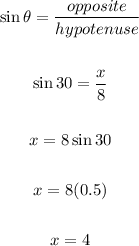
To solve for y, we have:

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \\ \tan 60=(x)/(y) \\ \\ \tan 60=(4)/(y) \\ \\ \text{Multiply both sid}es\text{ by y:} \\ y\tan 60=(4)/(y)\ast y \\ \\ y\tan 60=4 \\ \\ \text{Divide both sides by tan60} \\ \\ (y\tan 60)/(\tan 60)=(4)/(\tan60) \\ \\ \\ y=(4)/(\tan 60) \end{gathered}`

Solving further:

`\begin{gathered} y=\frac{4}{\sqrt[]{3}} \\ \\ \end{gathered}`

Multiply both numerator and denominator by √3:

`\begin{gathered} y=\frac{4}{\sqrt[]{3}}\ast\frac{\sqrt[]{3}}{\sqrt[]{3}} \\ \\ y=\frac{4\sqrt[]{3}}{3} \end{gathered}`

ANSWER:

`\begin{gathered} x=4 \\ \\ y=\frac{4\sqrt[]{3}}{3} \end{gathered}`