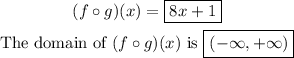Question

Consider the following solutions Please help on my question I’m confused

Answer 1

The function f(x) and g(x) is given as follows:

`f(x)=4x+5;\; g(x)=2x-1`

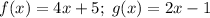
The composite function is defined as:

`(f\circ g)(x)=f(g(x))`

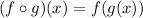
Replace x with g(x) in the expression given for f(x):

`f(g(x))=4(g(x))+5`

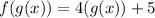
Substitute g(x)=2x-1 into the right-hand side of the equation:

`\begin{gathered} f(g(x))=4(2x-1)+5 \\ \Rightarrow f(g(x))=8x-4+5=8x+1 \end{gathered}`

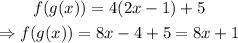
Recall that,

`\begin{gathered} (f\circ g)(x)=f(g(x)) \\ \Rightarrow(f\circ g)(x)=8x+1 \end{gathered}`

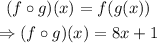
Notice that the composite function is a polynomial function of degree one (linear).

Recall also, that the domain of all polynomial functions is the set of real numbers.

Hence, the domain of the composite function (fog)(x) is the set of real numbers.

The set of real numbers in interval form is:

`(-\infty,+\infty)`

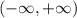
The answer is:

`\begin{gathered} (f\circ g)(x)=\boxed{8x+1} \\ \text{The domain of }(f\circ g)(x)\text{ is }\boxed{(-\infty,+\infty)} \end{gathered}`