Question A.
The initial population ocurrs at t=0. Then, by substituting this value into the given model ,we get
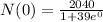
which gives

then, the answer is 51 owls.
Question B.
The limits when t approaches to + infinity is
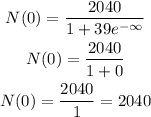
then, the answer is 2040 owls.
Question 15.
In this case, we need to find t when N(t) is 950, that is,
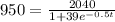
By moving the denominator to the left hand side, we have
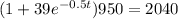
then, by moving 950 to the right hand side, we obtain
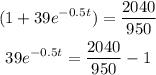
which is

so, we get
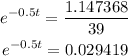
By applying natural logarithms to both sides, we have
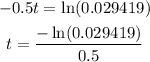
then, the answer is
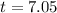
By rounding o the neares interger, the answer is 7 years