Question

Find the inverse of the function. Is the inverse a function? Simplify your answer.F(x)=2x-1f^-1(x)=

Answer 1

The definition of the inverse function is

`\begin{gathered} f(f^(-1)(x))=x \\ \text{and} \\ f^(-1)(f(y))=y \end{gathered}`

In our case,

`f(x)=2x-1`

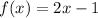
Then,

`\begin{gathered} f^(-1)(f(x))=x \\ \Rightarrow f^(-1)(2x-1)=x \\ \Rightarrow f^(-1)(x)=(x+1)/(2) \end{gathered}`

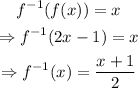
We need to verify this result using the other equality as shown below

`\begin{gathered} f^(-1)(x)=(x+1)/(2) \\ \Rightarrow f(f^(-1)(x))=f((x+1)/(2))=2((x+1)/(2))-1=x+1-1=x \\ \Rightarrow f(f^(-1)(x))=x \end{gathered}`

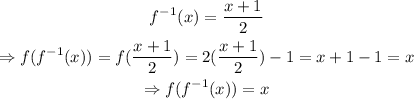
Therefore,

`\Rightarrow f^(-1)(x)=(x+1)/(2)`

The inverse function is f^-1(x)=(x+1)/2.

We say that a relation is a function if, for x in the domain of f, there is only one value of f(x).

In our case, notice that for any value of x, there is only one value of (x+1)/2=x/2+1/2.

The function is indeed a function, it is a straight line on the plane that is not parallel to the y-axis.

The inverse f^-1(x) is indeed a function