Given the figure of the circle Q
As shown, ST is tangent to circle Q
So, ST is perpendicular to the radius QS
So, the triangle QST is a right-angle triangle
We can apply the Pythagorean theorem where the legs are QS and ST
And the hypotenuse is QT
The side lengths of the triangle are as follows:
QS = r
ST = 48
QT = r + 36
So, we can write the following equation:
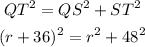
Expand then simplify the last expression:
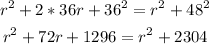
Combine the like terms then solve for (r):

So, the answer will be r = 14