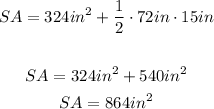Surface area of a square pyramid:
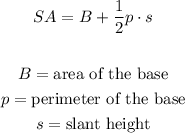
To find the surface area of the given pyramid as you don't have the length of the slant height, use the height of the pyramid and the radius of the base to form a right triangle and find the slant height:
Pythagorean theorem for the right triangle above:
![\begin{gathered} s^2=h^2+((1)/(2)b)^2 \\ \\ s=\sqrt[]{h^2+((1)/(2)b)^2} \\ \\ s=\sqrt[]{(12in)^2+((1)/(2)\cdot18in)^2} \\ \\ s=\sqrt[]{(12in)^2+(9in)^2} \\ \\ s=\sqrt[]{144in^2+81in^2} \\ \\ s=\sqrt[]{225in^2} \\ \\ s=15in \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/zo1ki64i41t7pb7ukbicp52iyz76pnc8zx.png)
Perimeter of the base is:
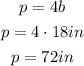
Area of the square base:
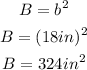
Then, the surface area of the given pyramid is