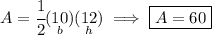Check the picture below.
well, we know the triangle is an isosceles, so it has twin sides coming from the "vertex" down to the "base", running an angle bisector from the "vertex" will give us a perpendicular to the "base", let's find its height.

so we simply need to get the area of a triangle whose base is 10 and height is 12.